Perpendicular Bisector
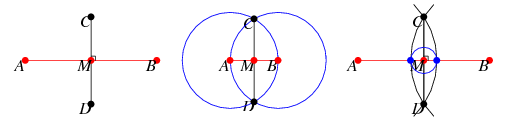
A perpendicular bisector 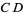 of a line segment
of a line segment 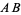 is a line segment perpendicular to
is a line segment perpendicular to 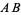 and passing through the midpoint
and passing through the midpoint 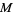 of
of 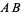 (left figure). The perpendicular bisector of a line segment can be constructed using a compass by drawing circles centered at
(left figure). The perpendicular bisector of a line segment can be constructed using a compass by drawing circles centered at 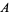 and
and 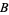 with radius
with radius 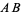 and connecting their two intersections. This line segment crosses
and connecting their two intersections. This line segment crosses 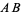 at the midpoint
at the midpoint 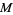 of
of 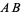 (middle figure). If the midpoint
(middle figure). If the midpoint 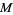 is known, then the perpendicular bisector can be constructed by drawing a small auxiliary circle around
is known, then the perpendicular bisector can be constructed by drawing a small auxiliary circle around 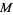 , then drawing an arc from each endpoint that crosses the line
, then drawing an arc from each endpoint that crosses the line 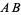 at the farthest intersection of the circle with the line (i.e., arcs with radii
at the farthest intersection of the circle with the line (i.e., arcs with radii 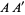 and
and 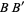 respectively). Connecting the intersections of the arcs then gives the perpendicular bisector
respectively). Connecting the intersections of the arcs then gives the perpendicular bisector 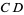 (right figure). Note that if the classical construction requirement that compasses be collapsible is dropped, then the auxiliary circle can be omitted and the rigid compass can be used to immediately draw the two arcs using any radius larger that half the length of
(right figure). Note that if the classical construction requirement that compasses be collapsible is dropped, then the auxiliary circle can be omitted and the rigid compass can be used to immediately draw the two arcs using any radius larger that half the length of 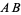 .Angle Bisector
.Angle Bisector
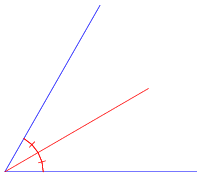
The (interior) bisector of an angle, also called the internal angle bisector (Kimberling 1998, pp. 11-12), is the line or line segment that divides the angle into two equal parts.
A. Constructing Perpendicular Bisector
B Angles Bisector
No comments:
Post a Comment