Mock Test solution - last few question

Revision answer key

JiaEn, Valery Poster

Pg 9 Example 5

Example 5, Page 9

A/N: If you still have doubts, you can always refer to your TI-Nspire "SET3" document for the more detailed version ^^

Example 7

S(square) is a subset of Q(rectangle).
This is true. A rectangle is defined as having four sides while a square is defined as having four equal sides (both with sides intersecting at 90 degrees). Since the square fulfills a rectangle's criteria but a rectangle does not fulfill a square's criteria, we can say S(square) is a subset of Q(rectangle).

R(rhombuses) is a subset of P(parallelograms).
This is true. A parallelogram is defined as having four sides with opposite sides being parallel while a rhombus is described as having four equal sides with opposite sides being parallel. Since a rhombus fulfills a parallelogram's criteria while a parallelogram fulfills a rhombi's criteria, we can say R(rhombuses) is a subset of P(parallelograms).

T(trapeziums) is not a subset of S, Q, R, P.
A trapezium is a quadrilateral with no sides parallel. Since the rest of the sets are quadrilaterals with parallel lines, we can say T(trapeziums) is not a subset of S, Q, R, P.

Q is a subset of P.
This is true. A parallelogram is a 4-sided shape where opposites sides are parallel. Rectangle fulfills the criteria, hence it is a subset of P. A rectangle's corners must be 90 degrees, and since a parallelogram does not fulfill that criteria, it cannot be a subset of Q.

Therefore, Wai Kit's venn diagram is not right and Mr. Johari's diagram is correct!

However, a square is a rhombus but a rhombus is not a rectangle. So how do we draw a venn diagram in this case? (Mr. Johari please help!)

Done by Carissa Liew

Maths PT Group 5 Bowen, Yan Feng and Ryan S207

Maths PT Group 6 Praveen (8) and Darshan (11) S207

Performance Task 3: Anti-Gambling Campaign

SET Theory CN-ECT activities

EOY Information

Here are some information about the paper:

Duration: 2 hr 30 min
Total marks: 100

40% of paper on Term 1 and 2 topics:

• Algebra and algebraic fractions
• Linear graphs
• Quadratic equations and graphs
• Area, perimeter, volume and surface area
• Pythagoras' Theorem
• Indices

60% of paper on Term 3 and 4 topics:

• Standard form
• Congruence and Similarity
• Area and volume of similar figures and solids
• Basic trigonometry
• Matrices
• Probability
• Simultaneous equations and graphs
• Set notation and venn diagrams
• Direct and inverse proportion

Set Language - CN-ECT Activity 2

Set Language - Activity 1 CN-ECT

Set Theory - Task - A Visual Presentation and Recommendation

Mini Non-graded Performance Task : A Visual Presentation and Recommendation

You are the registrar of School of Science and Technology, Singapore (SST). 

Since you have limited classrooms for classes, the school principal asked you to conduct a survey about the Applied Subjects you must offer for students.

Survey Results

After conducting a survey on 100 students, you obtained the following data: 

40 students plan to enroll in Media Studies (M), 

27 students prefer Fundamental of Electronic (F), and 

23 students want to take Biotechnology (B). 

Meanwhile 8 students prefer Media Studies (M) and Fundamental of Electronic (F), 

10 students prefer Biotechnology (B) and Fundamental of Electronic (F), and 

6 students prefer Biotechnology (B) and Media Studies (M), respectively. 

Then you also found out that 5 students would like to enroll in all the three subjects, while 10 students prefer other subjects. 

The principal required you to make a visual presentation of the data and a recommendation about the subjects to be offered.

Your presentation will be judged by the principal and the different department heads. Thus, make sure that it is clear, organized, accurate, and complete.

Venn diagram from oes_217

Performance Task 3

Probability Summary

Source: http://www.idomaths.com/probability3.php

 

Group 4 Example 15

Method: Probability Tree
3^3=27 (Total Possible Outcomes)
Number of 9s in Total Possible Outcomes: 7

Probability of score being 9: 7/27

Group 4 example 14

Example 14

a) P(one odd one even) = 18/36 = 1/2

b) P(same number) = 6/36 = 1/6   

Probability Group Activity - Group 3

Mini Task 4:

(a) Flipping a coin and getting heads, then flipping it again and getting tails

Ans: Independent.  Flipping heads the first time does not mean that the coin will be more/less likely to land tails the second time. The chances are still 1/2.

(b) Rolling doubles with two dice, then rolling doubles again.

Ans: Independant. Rolling doubles the first time does not make it more/less likely that a double will be rolled a second time. The dice cannot "remember" its previous result and change the next result.

(c) Drawing (and removing) two aces from a normal deck cards, then drawing kings.

Ans: Dependant. After removing the 2 aces, there are less cards in the deck, so the deck "remembers" that 2 aces are already picked, so it is more likely that a king will be picked.

(d) Drawing (and removing) a red ball initially containing two red balls and three white balls, then drawing a white ball.

Ans: Dependent. After removing the first red ball, there are less balls in the bag, so there is a higher chance of picking a white ball.

Mini Task 5:

(a) 13/100 x 8/100 = 13/1250

(b) 1/6 x 1/6 = 1/36

(c) 1/52 x 1/52 = 1/2704

(d) 1/100 x 1/100 = 1/10000

Example 13

P(Getting heads 3 times in 3 tosses)

= 1/2 x 1/2 x 1/2

= 1/8

Links:

http://www.mathgoodies.com/lessons/vol6/independent_events.html

http://www.mathgoodies.com/lessons/vol6/mutually_exclusive.html

Maths groupwork 2

Mutually exclusive are when 2 factors happens at a time but not simultaneously.For example when a person flips a coin,the results will be either heads or tails but not both,taking in account that it will not land in the center.Since it lands on heads,it cannot be tails.Another example is "it rained on Tuesday" and "it did not rain on Tuesday" are mutually exclusive events.

GROUP 1

Combined events are two or more events occurring at the same time or one after the other.

One example is:

(12 Possibilities)

Heads 1	Heads 2	Heads 3	Heads 4	Heads 5	Heads 6
Tails 1	Tails 2	Tails 3	Tails 4	Tails 5	Tails 6

There are 6 possible die outcomes each having a further 2 coin outcomes, giving a combined outcome of 12 possibilities. Therefore the probability of throwing a six and 'heads' is one outcome in twelve: . If the problem was changed to the possibility of throwing an odd number and 'tails', the table will show that this may occur 3 times, (1 tails, 3 tails, 5 tails) out of twelve outcomes, and therefore the probability is reduces to 312, or .

Another example is:
In a drawer, there are some white socks and some black socks. Tim takes out one sock and then a second. Draw a tree diagram to show the possible outcomes.

Example 10 Solution:

Probability Group activity

Discussion time: 20 minutes
Presentation of findings: 10 minutes
Comments: 10 minutes

Proportion : Direct and Inverse Answer Key

Construction

Definition

Perpendicular Bisector

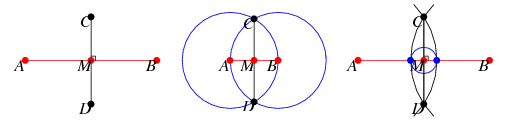
A perpendicular bisector 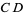 of a line segment  is a line segment perpendicular to 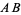 and passing through the midpoint  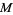of 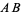(left figure). The perpendicular bisector of a line segment can be constructed using a compass by drawing circles centered at  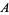and 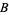with radius  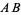and connecting their two intersections. This line segment crosses  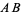at the midpoint  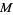of 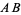 (middle figure). If the midpoint  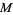is known, then the perpendicular bisector can be constructed by drawing a small auxiliary circle around 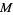, then drawing an arc from each endpoint that crosses the line  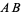at the farthest intersection of the circle with the line (i.e., arcs with radii  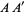and 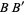respectively). Connecting the intersections of the arcs then gives the perpendicular bisector  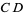(right figure). Note that if the classical construction requirement that compasses be collapsible is dropped, then the auxiliary circle can be omitted and the rigid compass can be used to immediately draw the two arcs using any radius larger that half the length of 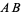.Angle Bisector

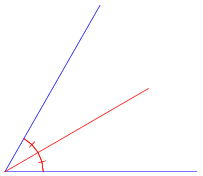
The (interior) bisector of an angle, also called the internal angle bisector (Kimberling 1998, pp. 11-12), is the line or line segment that divides the angle into two equal parts.

 A. Constructing Perpendicular Bisector  

B Angles Bisector